Let's start with an example: every 1 has at least two 0s following immediately after. Reverse: every 1 has at least two 0s preceding it.

Again, once we know the first, we can do its reverse mechanically (using Non Deterministic FSM). Notice that this is not the minimised FSM (generally we should be aiming for it).

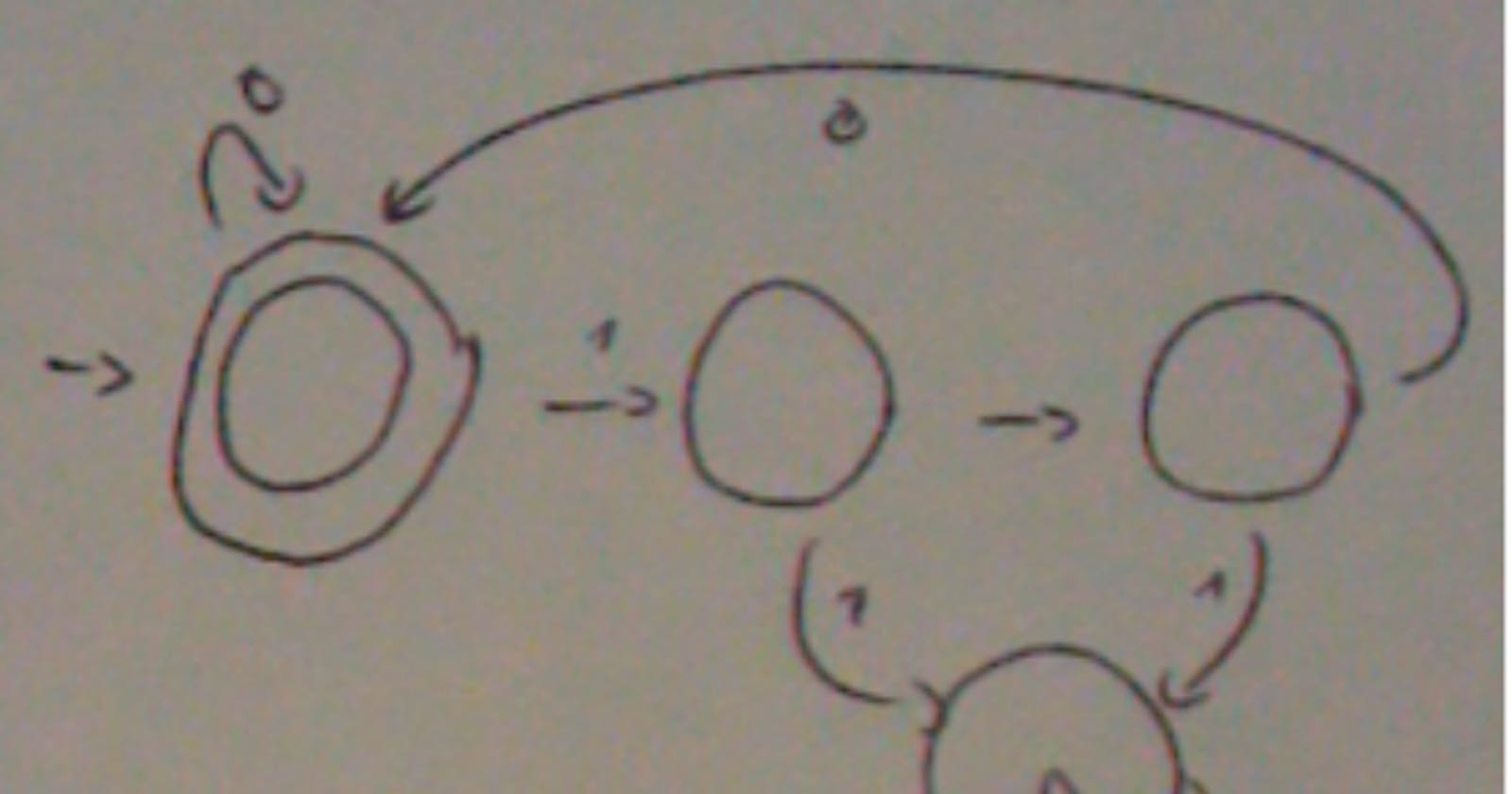
The minimised FSM for the last exercise from Lesson 1 looks like this:

Another equivalent FSM is this:

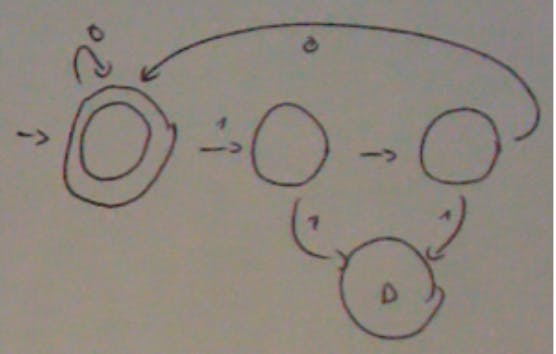
Note: complement means all the things that are not in our set.

Any set that has a FSM is called a regular set (i.e. any set of which you can make a FSM of). After an operation on a set (e.g. complement), if I get back a set that is also a regular set (always) then we say that the collection of sets are closed under complement (closed under “operation”) - in other words, after we do an operation on a set we always get something that a FSM can accept. The proof for closed under complement (for complement operation) is easy: take a set and reverse its final with non final states. Regular sets are also closed under reversal.

If you want to make a FSM for a reverse of a set, then we have to reverse everything: final state becomes the initial state, all the arrows are reversed and you start where you end.

Important: in the figure above since we have two final states our reversed machine needs to be able to reverse from either one of the states and end up in the other, so that’s why we need two start states (but since it’s not allowed we do it with an extra state).

More about this reversal: we need to start from where the first machine ended and end where the first machine started for every input, always. If we take e*psilon*, then the first machine starts from left and ends in left, we need to be able to do the same since start is the same as end.

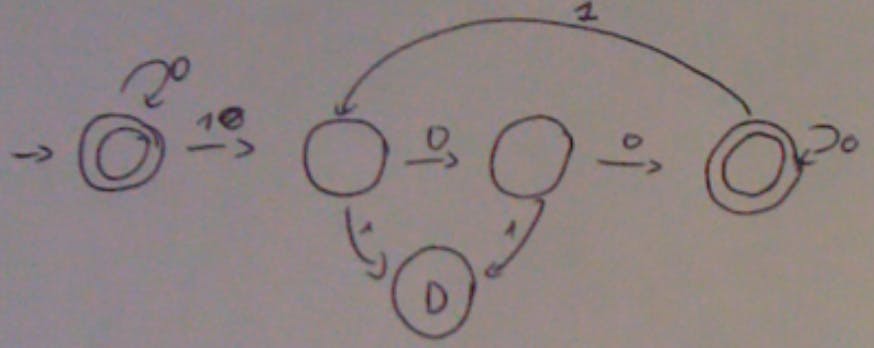
Notice that the Dead state has no connection to either start states so there’s no reason to draw it. Every string that has at least two 0’s and a 1 are accepted. It’s a ND FSM. We can see that our previous non-reversed deterministic machine had two final states and this one has one, why? It’s because of the fact that it’s non-deterministic, that is, we don’t need two states to accept the empty string AND non-empty strings. When we convert it to a non-deterministic machine we will have more than one state.

Note: you can always make a ND machine that has only one state (have e transitions to a final state).

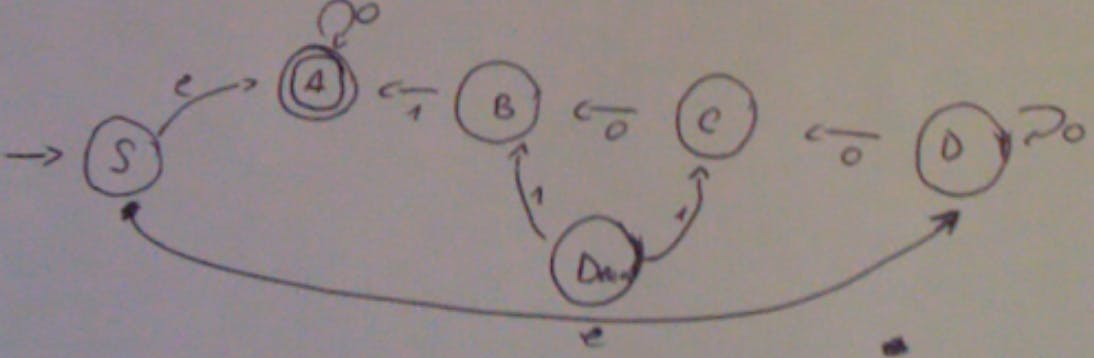
To turn this ND FSM in a deterministic FSM:

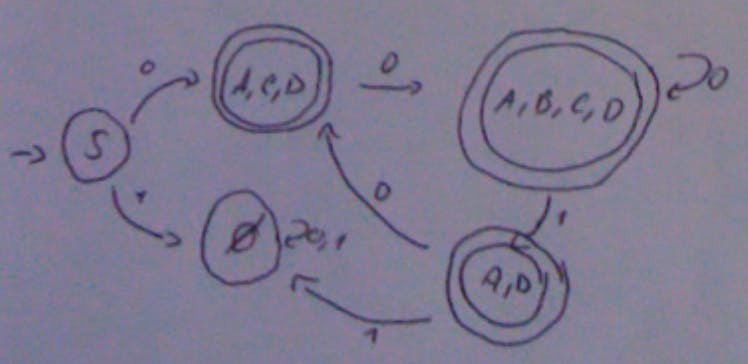
Starting from S and processing a 0 (only one) I get A,C,D because in my ND FSM I could get A (I start there) or start from D and move to C with a 0. And so forth. Notice that if at the S I get a 1 there are no states in which I find myself. The final states of this deterministic FSM are all ones that contain the final state of the ND FSM. The dead state is there for when we start with a 1.

Closures

Union (closure under union)

We need to find the even number of 0 and numbers containing 101. Drawing this machine from scratch might be a bit difficult; an easier way would be to use union:

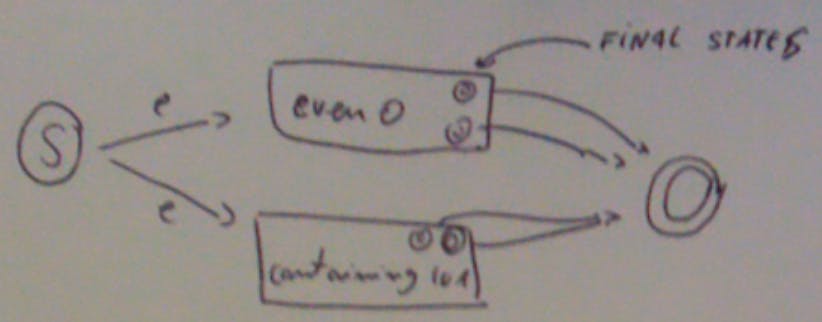
If there’s a way to accept the string because it contains an even number of 0s choose the first box; if there’s a way to accept the string because it contains an even number of 1s choose the second. The final states of those machines of which I ignore the details would bring me to the final state of the two machines. It’s a ND FSM.

Concatenation means having the number start with something and end with something else - in our example the concatenation is the number with even 0 that end in 101 (even zeros before 101). We do it by making the final states of the first machine go to the start state of the second one. This is of course non-deterministic.

Intersection (De Morgan)

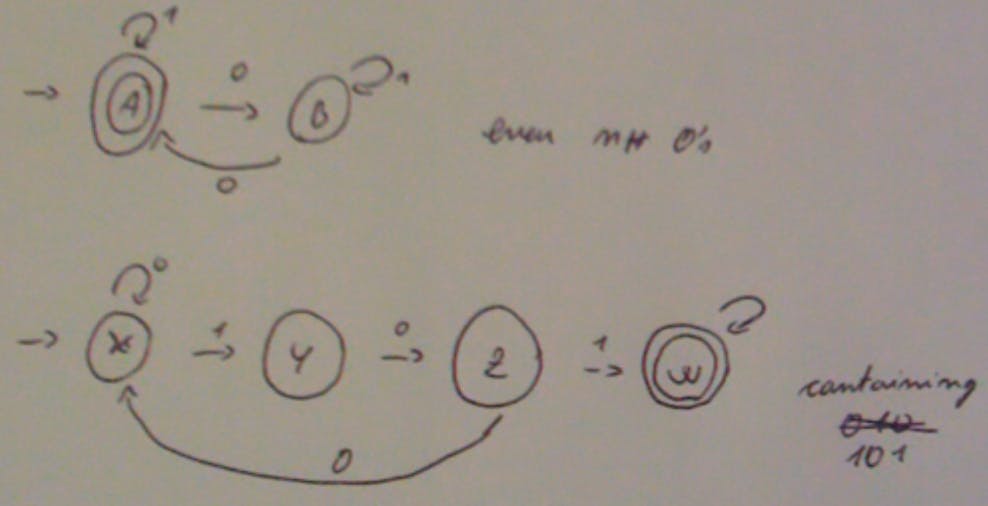
If we wanted to do the intersection of these two with a deterministic FSM we would get a total of 2 4 = 8 states; we multiply the number of states of both machines. The final states of the intersection will be only a *single state with both the final states from both machines.

Note non-determinism doesn’t mix well with intersection. It mixes well with OR not AND.

We need a way to prove that something can be modelled with a FSM.